Sistema de numeración hexadecimal

Sistema de numeración hexadecimal

En el sistema hexadecimal los números se representan con dieciséis símbolos: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E y F. Se utilizan los caracteres A, B, C, D, E y F representando las cantidades decima­les 10, 11, 12, 13, 14 y 15 respectivamente, porque no hay dígitos mayores que 9 en el sistema decimal. El valor de cada uno de estos símbolos depende, como es lógico, de su posición, que se calcula mediante potencias de base 16.
Calculemos, a modo de ejemplo, el valor del número hexadecimal 1A3F16:

1A3F16 = 1*163 + A*162 + 3*161 + F*160

1*4096 + 10*256 + 3*16 + 15*1 = 6719

1A3F16 = 671910


Ejercicio 7:
Expresa en el sistema decimal las siguientes cifras hexadecimales: 2BC516,  10016,  1FF16


Ensayemos, utilizando la técnica habitual de divisiones sucesivas, la conversión de un número decimal a hexadecimal. Por ejemplo, para convertir a hexadecimal del número 173510 será necesario hacer las siguientes divisiones:


1735 : 16 = 108    Resto: 7
108 : 16 = 6           Resto: C es decir, 1210
6 : 16 = 0                Resto: 6

De ahí que, tomando los restos en orden inverso, resolvemos el número en hexadecimal:

173510 = 6C716


Ejercicio 8:
Convierte al sistema hexadecimal los siguientes números decimales: 351910, 102410, 409510

Sistema de numeración hexadecimal

Sistema de numeración decimal

Sistema de numeración decimal:

El sistema de numeración que utiliza­mos habitualmente es el decimal, que se compone de diez símbolos o dígi­tos (0, 1, 2, 3, 4, 5, 6, 7, 8 y 9) a los que otorga un valor dependiendo de la posición que ocupen en la cifra: unidades, decenas, centenas, millares, etc.
El valor de cada dígito está asociado al de una potencia de base 10, número que coincide con la cantidad de símbolos o dígitos del sistema decimal, y un exponente igual a la posición que ocupa el dígito menos uno, contando desde la de­recha.
En el sistema decimal el número 528, por ejemplo, significa:

5 centenas + 2 decenas + 8 unidades, es decir:

5*102 + 2*101 + 8*100 o, lo que es lo mismo:

500 + 20 + 8 = 528


En el caso de números con decimales, la situación es análoga aunque, en este caso, algunos exponentes de las potencias serán negativos, concreta­mente el de los dígitos colocados a la derecha del separador decimal. Por ejemplo, el número 8245,97 se calcularía como:

8 millares + 2 centenas + 4 decenas + 5 unidades + 9 décimos + 7 céntimos

8*103 + 2*102 + 4*101 + 5*100 + 9*10-1 + 7*10-2, es decir:

8000 + 200 + 40 + 5 + 0,9 + 0,07 = 8245,97


Sistema de numeración decimal

Sistema de numeración octal

Sistema de numeración octal

El inconveniente de la codificación binaria es que la representación de algunos números resulta muy larga. Por este motivo se utilizan otros sistemas de numeración que resulten más cómodos de escribir: el sistema octal y el sistema hexadecimal. Afortunadamente, resulta muy fácil convertir un número binario a octal o a hexadecimal.
En el sistema de numeración octal, los números se representan mediante ocho dígitos diferentes: 0, 1, 2, 3, 4, 5, 6 y 7. Cada dígito tiene, naturalmente, un valor distinto dependiendo del lu­gar que ocupen. El valor de cada una de las posiciones viene determinado por las potencias de base 8.
Por ejemplo, el número octal 2738 tiene un valor que se calcula así:

2*83 + 7*82 + 3*81 = 2*512 + 7*64 + 3*8 = 149610

2738 = 149610


 Conversión de un número decimal a octal

La conversión de un número decimal a octal se hace con la misma técnica que ya hemos utilizado en la conversión a binario, mediante divisiones sucesivas por 8 y colocando los restos obtenidos en orden inverso. Por ejemplo, para escribir en octal el número decimal 12210 tendremos que hacer las siguientes divisiones:

122 : 8 = 15     Resto: 2
15 : 8 = 1           Resto: 7
1 : 8 = 0               Resto: 1
Tomando los restos obtenidos en orden inverso tendremos la cifra octal:

12210 = 1728

Ejercicio 5:
Convierte los siguientes números decimales en octales:  6310,   51310,   11910


 Conversión octal a decimal

La conversión de un número octal a decimal es igualmente sencilla, conociendo el peso de cada posición en una cifra octal. Por ejemplo, para convertir el número 2378 a decimal basta con desarrollar el valor de cada dígito:

2*82 + 3*81 + 7*80 = 128 + 24 + 7 = 15910

2378 = 15910


Ejercicio 6:
Convierte al sistema decimal los siguientes números octales: 458,   1258,   6258


Sistema de numeración octal

Sistema de numeración binario

Sistema de numeración binario.

El sistema de numeración binario utiliza sólo dos dígitos, el cero (0) y el uno (1).
En una cifra binaria, cada dígito tiene distinto valor dependiendo de la posición que ocupe. El valor de cada posición es el de una potencia de base 2, elevada a un exponente igual a la posición del dígito menos uno. Se puede observar que, tal y como ocurría con el sistema decimal, la base de la potencia coincide con la cantidad de dígitos utilizados (2) para representar los números.
De acuerdo con estas reglas, el número binario 1011 tiene un valor que se calcula así:

1*23 + 0*22 + 1*21 + 1*20 , es decir:

8 + 0 + 2 + 1 = 11

y para expresar que ambas cifras describen la misma cantidad lo escribimos así:

10112 = 1110


 Conversión entre números decimales y binarios

Convertir un número decimal al sistema binario es muy sencillo: basta con realizar divisiones sucesivas por 2 y escribir los restos obtenidos en cada división en orden inverso al que han sido obtenidos.
Por ejemplo, para convertir al sistema binario el número 7710 haremos una serie de divisiones que arrojarán los restos siguientes:
77 : 2 = 38 Resto: 1
38 : 2 = 19 Resto: 0
19 : 2 = 9 Resto: 1
9 : 2 = 4 Resto: 1
4 : 2 = 2 Resto: 0
2 : 2 = 1 Resto: 0
1 : 2 = 0 Resto: 1
y, tomando los restos en orden inverso obtenemos la cifra binaria:

7710 = 10011012

Ejercicio 1:
Expresa, en código binario, los números decimales siguientes:  191, 25, 67, 99, 135, 276


 El tamaño de las cifras binarias

La cantidad de dígitos necesarios para representar un número en el sistema binario es mayor que en el sistema decimal. En el ejemplo del párrafo anterior, para representar el número 77, que en el sistema decimal está compuesto tan sólo por dos dígitos, han hecho falta siete dígitos en binario.
Para representar números grandes harán falta muchos más dígitos. Por ejemplo, para representar números mayores de 255 se necesitarán más de ocho dígitos, porque 28 = 256 y podemos afirmar, por tanto, que 255 es el número más grande que puede representarse con ocho dígitos.
Como regla general, con n dígitos binarios pueden representarse un máximo de 2n, números. El número más grande que puede escribirse con n dígitos es una unidad menos, es decir, 2n – 1. Con cuatro bits, por ejemplo, pueden representarse un total de 16 números, porque 24 = 16 y el mayor de dichos números es el 15, porque 24-1 = 15.


Ejercicio 2:
Averigua cuántos números pueden representarse con 8, 10, 16 y 32 bits y cuál es el número más grande que puede escribirse en cada caso.


Ejercicio 3:
Dados dos números binarios: 01001000 y 01000100 ¿Cuál de ellos es el mayor? ¿Podrías compararlos sin necesidad de convertirlos al sistema decimal?

 Conversión de binario a decimal

El proceso para convertir un número del sistema binario al decimal es aún más sencillo; basta con desarrollar el número, teniendo en cuenta el valor de cada dígito en su posición, que es el de una potencia de 2, cuyo exponente es 0 en el bit situado más a la derecha, y se incrementa en una unidad según vamos avanzando posiciones hacia la izquierda.
Por ejemplo, para convertir el número binario 10100112 a decimal, lo desarrollamos teniendo en cuenta el valor de cada bit:

1*26 + 0*25 + 1*24 + 0*23 + 0*22 + 1*21 + 1*20 = 83

10100112 = 8310

Ejercicio 4:
Expresa, en el sistema decimal, los siguientes números binarios:
110111, 111000, 010101, 101010, 1111110



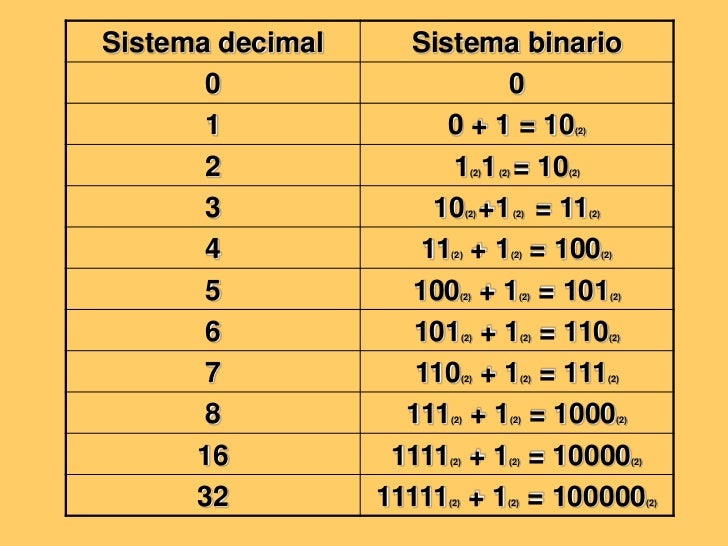sistema de numeracion binario

Sistema de control de retroalimentacion

Los sistemas de control según la Teoría CIBERNETICA se aplican en esencia para los organismos vivos, las máquinas y las organizaciones. Estos sistemas fueron relacionados por primera vez en 1948 por Norbert Wiener en su obra Cibernética y Sociedad con aplicación en la teoría de los mecanismos de control. Un sistema de control está definido como un conjunto de componentes que pueden regular su propia conducta o la de otro sistema con el fin de lograr un funcionamiento predeterminado, de modo que se reduzcan las probabilidades de fallos y se obtengan los resultados buscados

Los sistemas de control realimentados se denominan también sistemas de control de lazo cerrado. En la práctica, los términos control realimentado y control en lazo cerrado se usan indistintamente.

En un sistema de control en lazo cerrado, se alimenta al controlador la señal de error de actuación, que es la diferencia entre la señal de entrada y la salida de realimentación (que puede ser la señal de salida misma o una función de la señal de salida y sus derivadas o/y integrales) a fin de reducir el error y llevar la salida del sistema a un valor conveniente. El término control en lazo cerrado siempre implica el uso de una acción de control realimentando para reducir el error del sistema.

Sistema de control de retroalimentacion

Sistema de control de lazo cerrado

Son los sistemas en los que la acción de control está en función de la señal de salida. Los sistemas de circuito cerrado usan la retroalimentación desde un resultado final para ajustar la acción de control en consecuencia.

El control en lazo cerrado es imprescindible cuando se da alguna de las siguientes circunstancias:

• Cuando un proceso no es posible de regular por el hombre.
• Una producción a gran escala que exige grandes instalaciones y el hombre no es capaz de manejar.
• Vigilar un proceso es especialmente difícil en algunos casos y requiere una atención que el hombre puede perder fácilmente por cansancio o despiste, con los consiguientes riesgos que ello pueda ocasionar al trabajador y al proceso.

Sus características son:

• Ser complejos, pero amplios en cantidad de parámetros.
• La salida se compara con la entrada y le afecta para el control del sistema.
• Su propiedad de retroalimentación.
• Ser más estable a perturbaciones y variaciones internas.

Un ejemplo de un sistema de control de lazo cerrado sería el termotanque de agua que utilizamos para bañarnos.

Otro ejemplo sería un regulador de nivel de gran sensibilidad de un depósito. El movimiento de la boya produce más o menos obstrucción en un chorro de aire o gas a baja presión. Esto se traduce en cambios de presión que afectan a la membrana de la válvula de paso, haciendo que se abra más cuanto más cerca se encuentre del nivel máximo.

sistema de control de lazo cerrado

Sistema de control de lazo abierto

Es aquel sistema en que solo actúa el proceso sobre la señal de entrada y da como resultado una señal de salida independiente a la señal de entrada, pero basada en la primera. Esto significa que no hay retroalimentación hacia el controlador para que éste pueda ajustar la acción de control. Es decir, la señal de salida no se convierte en señal de entrada para el controlador.

• Ejemplo 1: Un tanque con una manguera de jardín. Mientras que la llave siga abierta, el agua fluirá. La altura del agua en el tanque no puede hacer que la llave se cierre y por tanto no nos sirve para un proceso que necesite de un control de contenido o concentración.
• Ejemplo 2: Al hacer una tostada, lo que hacemos es controlar el tiempo de tostado de ella misma entrando una variable (en este caso el grado de tostado que queremos). En definitiva, el que nosotros introducimos como parámetro es el tiempo.

Estos sistemas se caracterizan por:

• Ser sencillos y de fácil concepto.
• Nada asegura su estabilidad ante una perturbación.
• La salida no se compara con la entrada.
• Ser afectado por las perturbaciones. Estas pueden ser tangibles o intangibles.
• La precisión depende de la previa calibración del sistema..

Sistema de control de lazo abierto